This bio-recipe describes the computation of various codon statistics with the purpose of discovering which frequencies deviates the most from their expected values. This comes under the general title of Codon Bias. In our terminology, a codon is a group of 3 bases which code for an amino acid (or for a stop codon). I.e. this is coding DNA or coding mRNA.
We will study these biases for yeast (baker's yeast or Saccharomyces cerevisiae). Since we are going to do several computations over the yeast genome, we will load a version of the genome which contains a protein (or conjectured protein) per entry. Each entry contains the DNA sequence and the amino acid sequence for its protein. We load the database with ReadDb.
ReadDb( '/home/darwin/DB/genomes/YEAST/yeast.db' );
Peptide file(/home/darwin/DB/genomes/YEAST/yeast.db(12985775), 6194 entries, 2902851 aminoacids)
In the first phase of this process we will collect all the frequencies that we will use later. These are the frequencies of amino acids, the frequencies of pairs of consecutive amino acids, the frequencies of the codons used and the frequencies of pairs of consecutive codons. The codons are encoded with an integer from 1 to 64 (called a CInt in Darwin) and the amino acids, as usual, are encoded with an integer from 1 to 20 (called Int in Darwin). These will be stored in the following arrays:
AAFreq := CreateArray( 1..20 ): AAPairs := CreateArray( 1..20, 1..20 ): Codons := CreateArray( 1..64 ): CodonCodon := CreateArray( 1..64, 1..64 ):
Now we will loop over all the entries and for each entry we will go sequentially over all the amino acids and in parallel over all the bases.
for e in Entries() do
tD := SearchTag(DNA,string(e));
tA := SearchTag(SEQ,string(e));
if length(tD) <> 3*length(tA)+3 then
error(tD,tA,'non matching lengths') fi;
we get the DNA and the amino acids and check that the lengths are consistent. To make the code a bit more efficient, we compute the codons' encoding only once and slide them to compute the counts for the pairs.
i1 := AToInt(tA[1]);
b123 := CodonToCInt(tD[1..3]);
for i to length(tA) do
AAFreq[i1] := AAFreq[i1] + 1;
Codons[b123] := Codons[b123] + 1;
if i=length(tA) then break fi;
i2 := AToInt(tA[i+1]);
b456 := CodonToCInt(tD[3*i+1..3*i+3]);
AAPairs[i1,i2] := AAPairs[i1,i2] + 1;
CodonCodon[b123,b456] := CodonCodon[b123,b456] + 1;
i1 := i2; b123 := b456;
od;
od:
It is a good practice to check the consistency of the counts. We do this by comparing against the total of amino acids and the total number of pairs.
nA := DB[TotAA];
nS := DB[TotEntries];
check := sum( Codons ) - nA,
sum( sum(CodonCodon[i]), i=1..64 ) - (nA-nS),
sum( sum(AAPairs[i]), i=1..20 ) - (nA-nS);
nA := 2902851 nS := 6194 check := 0, 0, 0
We now normalize the AAFreq and AAPairs frequencies by dividing them by their total count. This is our approximation of the probability of amino acid pairs.
AAPairs := AAPairs / (nA-nS): AAFreq := AAFreq / sum(AAFreq):
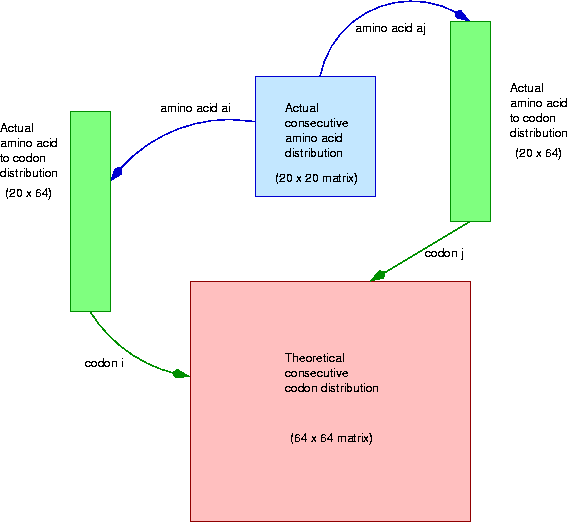
We are now ready to define the bias that we will observe. Each amino acid has its own probability of occurrence in the genome. It is understood and accepted that different amino acids have different frequencies. It is also understood and accepted that pairs of amino acids have a probability distribution that departs from the product of the individual probabilities. This is caused by the chemical and structural properties of amino acids, and is going to be taken as a given. Finally, amino acids are coded by different codons, and these are not equally probable (within an amino acid) either. Codon probabilities are probably affected by tRNA abundance and other unknown causes.
In principle, all the natural selection pressures operate on the amino acids and on the codon distribution per amino acid. But there is no known influence on codon bias over amino acid distribution, as these two events relatively indenpendent. In this analysis we find a surprising bias on the distribution of consecutive pairs of codons. This will be studied by computing the theoretical distribution of consecutive codon pairs from the codon distribution and the consecutive amino acid pairs and comparing it against the observed distribution.

The next loop computes the theoretical distribution of consecutive pairs of codons according to the above. Notice that the expression Codons[i] / AAFreq[ai] computes the particular codon frequency for a given amino acid. Again, it is a good idea to check that the matrix entries add up to 1.
TheoCodonCodon := CreateArray(1..64,1..64):
Codons := Codons / sum(Codons):
for i to 64 do
ai := CIntToInt(i);
if ai < 1 or ai > 20 then next fi;
for j to 64 do
aj := CIntToInt(j);
if aj < 1 or aj > 20 then next fi;
TheoCodonCodon[i,j] := Codons[i] / AAFreq[ai] * AAPairs[ai,aj] *
Codons[j] / AAFreq[aj]
od od:
check := sum(sum(TheoCodonCodon))-1;
check := -1.1102e-16
With the previous computations we can compare, for any particular codon, its expected against actual frequency. While this is our goal, it would be good to explore all possible codons or groups of codons. By a group of codons we do not mean an arbitrary group, but rather a pair of codons which ignores one particular base, i.e. we sum all the values for that position. We denote such positions with an asterisk, *, e.g. AC*TG* meaning that we add the 16 codons which have the given pattern together. We do this in the hope that if there is some effect that depends on some particular bases and not on others in the codon pairs, this groupings will magnify their significance. Computationally, we will designate the first 4 positions of an array to each base and the fifth position to be the sum of the first four. We do this for the actual and theoretical distributions. Before doing any additions we convert the arrays from two indices (two codons) to six bases.
SixBases := CreateArray(1..5,1..5,1..5,1..5,1..5,1..5):
TheoSixBases := CreateArray(1..5,1..5,1..5,1..5,1..5,1..5):
for b1 to 4 do for b2 to 4 do for b3 to 4 do
i1 := 16*(b1-1) + 4*(b2-1) + b3;
for b4 to 4 do for b5 to 4 do for b6 to 4 do
i2 := 16*(b4-1) + 4*(b5-1) + b6;
SixBases[b1,b2,b3,b4,b5,b6] := CodonCodon[i1,i2];
TheoSixBases[b1,b2,b3,b4,b5,b6] := TheoCodonCodon[i1,i2];
od od od
od od od;
check := sum(sum(sum(sum(sum(sum(SixBases)))))) - (nA-nS),
sum(sum(sum(sum(sum(sum(TheoSixBases)))))) - 1;
check := 0, 0
Having verified that the SixBases arrays add up to the right values we will now proceed to compute the fifth positions. We will write a function that does this sum for a particular set of indices. Notice that if there is no index valued at 5, the function does not do any work.
SummarizeCodon := proc( A:list, inds:list(posint) )
for i to length(inds) do if inds[i] = 5 then
inds2 := copy(inds);
s := 0;
for j to 4 do inds2[i] := j; s := s + A[op(inds2)] od;
A[op(inds)] := s
fi od;
end:
Since we want to modify the array inds passed as an argument while computing the sum, we make a copy of it. We now apply the function over all indices and on both arrays.
for b1 to 5 do for b2 to 5 do for b3 to 5 do
for b4 to 5 do for b5 to 5 do for b6 to 5 do
SummarizeCodon( SixBases, [b1,b2,b3,b4,b5,b6] );
SummarizeCodon( TheoSixBases, [b1,b2,b3,b4,b5,b6] );
od od od od od od;
check := SixBases[5,5,5,5,5,5]-(nA-nS), TheoSixBases[5,5,5,5,5,5]-1;
check := 0, 0
Again we check that the entry with all 5's is the sum of all the observations and the probability 1 respectively. Now we are ready to inspect the deviations. The number of entries for each group of six bases is binomially distributed. This distribution can be viewed as a balls in boxes model. The total number of balls is the total number of pairs, nA-nS and the probability is the theoretical probability in TheoSixBases. To compute the significance of the departure from the expected we want to compute the cumulative distribution. In this particular case, since some deviations are very significant, we use the function CumulativeStd which returns its result in standard deviations of an equivalent Normal(0,1) variable. (See ?CumulativeStd for more details). We will print all the values which have a very large deviation (larger than 50 std deviations) and store all of the ones larger than 20 std deviations for later sorting and analysis. The list called Symbol is used to simplify the conversion of an index to a base or *.
Symbol := ['A','C','G','T','*']:
Above20 := []:
printf( ' Codons std dev actual expected\n' );
for b1 to 5 do for b2 to 5 do for b3 to 5 do
for b4 to 5 do for b5 to 5 do for b6 to 5 do
pr := TheoSixBases[b1,b2,b3,b4,b5,b6];
if pr>=1 or pr<=0 then next fi;
np := (nA-nS)*pr;
std := CumulativeStd( Binomial(nA-nS,pr), SixBases[b1,b2,b3,b4,b5,b6]);
if |std| > 50 then
printf( ' %s%s%s %s%s%s %6.2f %9d %9.1f\n',
Symbol[b1], Symbol[b2], Symbol[b3],
Symbol[b4], Symbol[b5], Symbol[b6],
std, SixBases[b1,b2,b3,b4,b5,b6], np ) fi;
if |std| > 20 then
Above20 := append(Above20,[b1,b2,b3,b4,b5,b6,std]) fi
od od od
od od od;
Codons std dev actual expected C*T A** -53.05 32939 43447.5 *CC A** 56.49 57715 45285.0 *TC AA* 52.43 27045 19339.5 *TC A** 60.33 62466 48693.2 *TT AA* -63.41 22952 33879.1 *TT A** -71.69 65389 85174.8 **C AA* 64.02 89706 72095.5 **C A** 80.20 217348 183205.8 **C G** -63.03 136335 160260.5 **T AA* -72.23 98308 122206.7 **T AG* -53.06 39923 51381.3 **T A*A -54.59 75747 91525.5 **T A*G -53.79 48526 61223.1 **T A** -83.41 267017 310962.7 **T G*T 50.54 115359 99317.8 **T G** 66.46 306076 272470.0
As we can see, there are major deviations, which cannot be accepted under the proposed model as random variations. Actually anything above 4-5 standard deviations is immediately suspicious, the above values leave no room for doubt.
Finally we want to make a list, in decreasing order of significance, of the patterns. Since some patterns may be included in others, we would like to place these patterns in three columns: the patterns which appear for the first time, the patterns which are a subset of a pattern already listed and the patterns which are a superset of one already listed. To do this classification we need a function that determines if one pattern Includes another:
Includes := proc( a:list, b:list ) for i to 6 do if a[i] <> b[i] and a[i] <> 5 then return(false) fi od; true end:
Now we can print the lists:
Above20 := sort( Above20, x -> -|x[7]| ):
printf( ' initial subset of above superset of above\n' );
for i to 100 do
z := Above20[i];
for j to i-1 do
if Includes(z,Above20[j]) then
printf( CreateString(44) ); break
elif Includes(Above20[j],z) then
printf( CreateString(22) ); break
fi
od;
printf( ' %s%s%s %s%s%s %6.2f\n',
Symbol[z[1]], Symbol[z[2]], Symbol[z[3]],
Symbol[z[4]], Symbol[z[5]], Symbol[z[6]], z[7] )
od:
initial subset of above superset of above
**T A** -83.41
**C A** 80.20
**T AA* -72.23
*TT A** -71.69
**T G** 66.46
**C AA* 64.02
*TT AA* -63.41
**C G** -63.03
*TC A** 60.33
*CC A** 56.49
**T A*A -54.59
**T A*G -53.79
**T AG* -53.06
C*T A** -53.05
*TC AA* 52.43
**T G*T 50.54
*CT A** -49.80
CTT A** -48.76
*TT A*A -48.38
A*C A** 48.34
**T AAG -47.59
T*C A** 46.98
**C A*C 46.78
T*T A** -46.56
*TC G** -45.94
T*C G** -45.04
**C G*A -44.32
A*T G** 43.93
*GT G** 43.69
CTT T** 43.63
**T GC* 42.89
**C AAG 42.75
*TT A*G -42.35
*CT AA* -42.26
T*C AA* 41.80
A*T A** -41.53
T*T AA* -41.43
C*T AA* -40.60
*TG T** -40.26
**C GA* -40.15
TTC G** -40.11
**C A*T 40.00
CTT AA* -39.99
ATT A** -39.56
**T *AG -39.42
**C A*G 39.41
**A AG* 39.40
A*C AA* 39.10
TTG T** -39.06
ATC A** 38.32
**C GC* -38.07
*CC AA* 37.87
*TT AAG -37.78
C*T AG* -37.60
TTC A** 37.15
A*T AA* -37.09
*TT G** 36.84
TTC AA* 36.79
**T AAA -36.48
*TT AG* -36.39
*CC AT* 36.18
*TT AAA -36.14
*TT T** 36.11
G*C A** 35.54
*TC A*C 35.38
*GT G*T 35.28
*CT AG* -35.27
ATC AA* 35.25
*CC G** -34.95
TTT AA* -34.68
**C AC* 34.44
G*T G*T 34.40
ATT AA* -34.13
TTT A** -33.76
C*T A*A -33.64
**T G*C 33.30
**C AAA 33.19
**T AGA -32.98
**T GG* 32.95
*CC GA* -32.88
C*T T** 32.75
*CT A*A -32.66
T*T G** 32.59
**T *A* -32.58
G*C G** -32.36
TTG AA* 32.25
**C A*A 32.13
**C G*G -32.02
*TC GC* -31.93
**T T** 31.72
CTT A*A -31.71
*CC A*T 31.62
*TC A*T 31.61
G*T G** 31.57
GCC A** 31.56
*CT A*G -31.51
**T GCT 31.28
TCC A** 31.24
A*C A*C 31.21
*TC G*A -31.21
As a final exercise we will build an HTML table with the same information as above (but over the first 200 instead of 100). We use the Code() construct to enclose the codons so that an equal spacing font is used and so that spaces are preserved.
Rows := NULL:
for i to 200 do
z := Above20[i];
cc := Code(sprintf( '%s%s%s %s%s%s %5.1f',
Symbol[z[1]], Symbol[z[2]], Symbol[z[3]],
Symbol[z[4]], Symbol[z[5]], Symbol[z[6]], z[7] ));
for j to i-1 do
if Includes(z,Above20[j]) then
Rows := Rows, Row('','',cc); break
elif Includes(Above20[j],z) then
Rows := Rows, Row('',cc,''); break
fi
od;
if j >= i then Rows := Rows, Row(cc,'','') fi
od:
Table200 := Table( center, border,
ColAlign(c,c,c),
Row( 'initial', 'subset of previous', 'superset of previous' ),
Row( 'codons -- std devs', 'codons -- std devs',
'codons -- std devs' ), Rule, Rows ):
The table with the top 200 entries as it would be seen with the command View(HTML(TableOne)).
© 2005 by Gaston Gonnet, Informatik, ETH Zurich
Please cite as:
@techreport{ Gonnet-CodonBias,
author = {Gaston H. Gonnet},
title = {The most significant Codon Bias in Yeast},
month = { June },
year = {2003},
number = { 413 },
howpublished = { Electronic publication },
copyright = {code under the GNU General Public License},
institution = {Informatik, ETH, Zurich},
URL = { http://www.biorecipes.com/CodonBias/code.html }
}
Last updated on Fri Sep 2 17:10:22 2005 by GhG