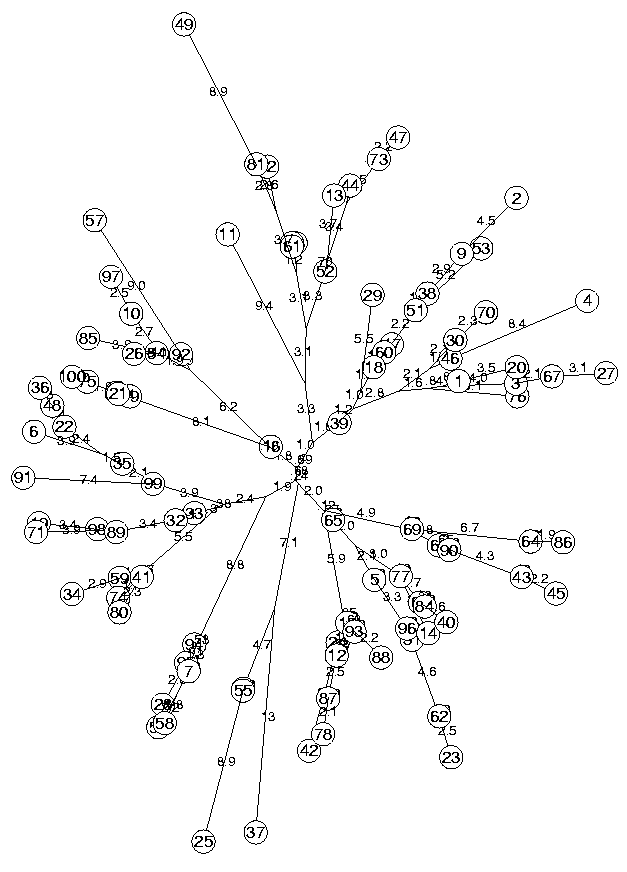
Darwin has a function to build phylogenetic trees based on distances called MinSquareTree. This function takes an all-against-all matrix of distances and constructs a tree which matches the distances on the tree with the distances of the matrix as best as possible. The approximation is best in the sense of least squares, that is, the sum of the squares of the errors in the distances is minimized. The description page of this function is:
?MinSquareTree
the following help files contain (approximately) the keyword: ?BootstrapTree ?ClusterRelPam ?DrawBisectTree ?DrawTree ?DrawUnrootedTree ?GapTree ------------
First we would like to generate a random distances tree and display it. We will assume that the short distances are more accurate than the long distances (something that is true with real trees) and model this by making the variance equal to the distances.
n := 100;
Dist := CreateArray(1..n,1..n):
for i to n do for j from i+1 to n do
Dist[i,j] := Dist[j,i] := 100*Rand() od od;
t := MinSquareTree( Dist, Dist ):
n := 100 MinLen not set, using 0.050494 dimensionless fitting index 252.5
The above produces the following tree which has no obvious structure (it is made of random distances!):

The function MinSquareTree printed two messages, the first one indicating that MinLen was not assigned, and a default value was used. This parameter ensures that the branches are not too short. Of course branches cannot be of length zero, but it is usually convenient (just for display purposes if anything), to set it to a value that will allow us to see the edges.
The second message shows a quality indicator of the tree 25.2890 which is the sum of the squares of the errors on the distances divided by (n-2)(n-3)/2, which is the number of degrees of freedom of the errors, if they would be random variables. So the sum of the squares of all the errors is:
MST_Qual*(n-2)*(n-3)/2;
120198.8513
Next we will verify this number, that is we will compute the distances over the tree and calculate the sum of squares. This is a good exercise in programming over recursive structures like trees. Since we want to compute distances of all nodes against each other, we should not use a brute force algorithm. We will use three functions that we describe here:
| - | DistanceOnTree The distance on the tree can be computed rather efficiently if we add some information to each node. So we are going to build a new tree, identical to the tree that we have, but with additional information in each node. As it turns out to be, it is enough to have the set of leaf numbers that are descendants of each node. |
| - | ExtendTree This function will add a set of all the descendant leaves to each node. This set of leaves nodes will be stored in the 4th position of each node (Tree or Leaf). |
| - | DistanceToLeaf To assist the computation of a distance between two leaves, we will compute the distance from an internal node to a Leaf. This function also uses the extra information in the 4th position of each node. |
DistanceOnTree := proc( t:Tree, i1:posint, i2:posint )
if {i1,i2} minus t[4] <> {} then error(i1,i2,'are not in tree') fi;
int := {i1,i2} intersect t[Left,4];
if length(int)=0 then procname( t[Right], i1, i2 )
elif length(int)=2 then procname( t[Left], i1, i2 )
else DistanceToLeaf(t,i1) + DistanceToLeaf(t,i2) fi
end:
The above code first checks that the subtree has both requested leaves. If it doesn't, it is an error. If it does, it also means that the node t is not a Leaf. We test whether the two leaves are on the right or left subtree, and if we have one in each, then we are ready to compute the distance.
ExtendTree := proc( t:Tree )
if type(t,Leaf) then Leaf( t[1], t[2], t[3], {t[3]} )
else tl := procname( t[Left] );
tr := procname( t[Right] );
Tree( tl, t[2], tr, tl[4] union tr[4] ) fi
end:
The above function just adds the set of descendants to each node in its 4th position.
DistanceToLeaf := proc( t:Tree, i:posint )
if not member(i,t[4]) then error(i,'Leaf is not in subtree')
elif type(t,Leaf) then 0
elif member(i,t[Left,4]) then
|t[Height]-t[Left,Height]| + procname(t[Left],i)
else |t[Height]-t[Right,Height]| + procname(t[Right],i) fi
end:
Finally, the third function checks whether the requested Leaf is in the subtree and then decides in 3 ways: whether it is there already (distance 0) or in the left or in the right. It applies itself recursively on the correct subtree.
Fist we test this function with an arbitrary pair of nodes.
et := ExtendTree(t): DistanceOnTree( et, 10, 20 ), Dist[10,20];
37.3968, 60.2250
Now we are ready to compute the differences and compare, (remember that we defined the variance as the distances themselves, so we have to divide the squares of the differences by the distances) and we see them in perfect agreement.
MST_Qual*(n-2)*(n-3)/2;
sum( sum( (DistanceOnTree(et,i,j)-Dist[i,j]) ^ 2 /
Dist[i,j], j=i+1..n ), i=1..n );
120198.8513 120198.8513
We will now build several trees over random distance matrices. It should be said that random distance matrices are a very challenging problem for the building algorithms, so in some sense these represent worst case results. We are interested in measuring two variables. First, we would like to know the average quality (for these trees, this is mostly curiosity, as we never have such trees in reality, but for other families of trees it could make more sense). Secondly, we will run once the default algorithm and then several random trials. When we run a random trial, the optimization starts from a random tree, and in some cases it could produce a better tree. We are interested in knowing how often we succeed with a better tree computed from a random start. So we prepare variables to store these results.
Labels := [ seq( i, i=1..n )]:
qual := Stat('MST quality index'):
MinLen := 0.1:
maxtr := 10;
hist := CreateArray(1..maxtr):
maxtr := 10
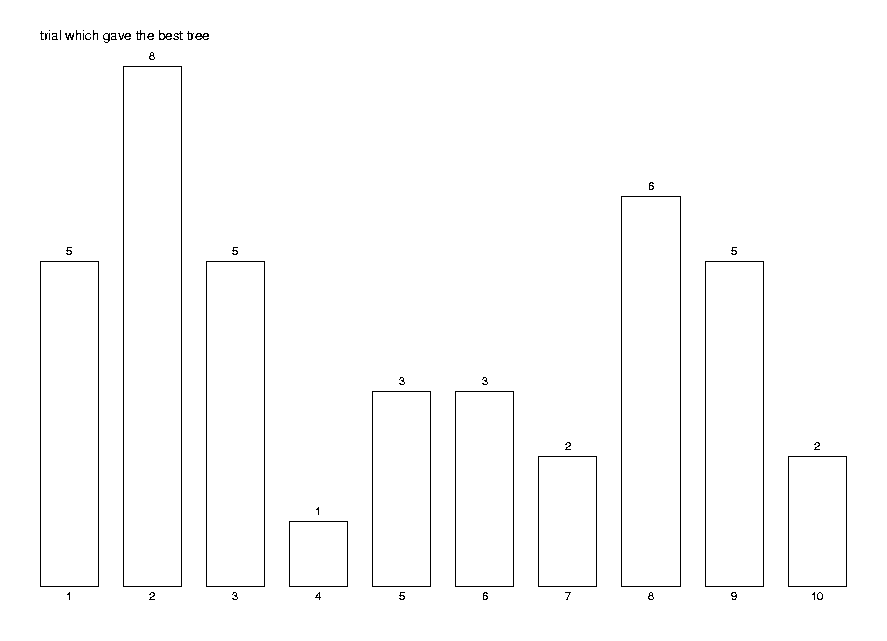
Now we will build trees over 40 different distance matrices, and for each matrix we will be run once with the default algorithm and 9 times with a random initial start. We will record the trial number of the best (lowest) quality obtained.
for iter to 40 do
Generate the random distances matrix
for i to n do for j from i+1 to n do
Dist[i,j] := Dist[j,i] := 100*Rand() od od;
First (default) tree, the rest random
MinSquareTree( Dist, Dist );
q := MST_Qual; trbest := 1;
for tr from 2 to maxtr do
MinSquareTree( Dist, Dist, Labels, Random );
if q > MST_Qual then q := MST_Qual; trbest := tr fi;
od;
hist[trbest] := hist[trbest]+1;
qual+q;
od:
bytes alloc=39485820, time=61.090
Print the quality statistics and a histogram of the most successful trial.
print(qual);
DrawHistogram(hist,[seq(i,i=1..maxtr)],
Title='trial which gave the best tree');
MST quality index: number of sample points=40 mean = 26.68 +- 0.23 variance = 0.53 +- 0.24 skewness=0.194185, excess=0.246919 minimum=24.9493, maximum=28.6197
The histogram shows that it is useful to try several trees, as the distribution is not as skewed to the left as we would like it to be. That is, quite often the best value is not the first computed.
It is interesting and relevant to see the distribution of the quality of a random distance tree. This will help us understand how concentrated the distribution is and how useful additional trials may be. To do this we generate 200 trees from the same distance matrix and plot the distribution of their qualities.
quals := []:
to 200 do
MinSquareTree( Dist, Dist, Labels, Random );
quals := append( quals, MST_Qual ) od:
DrawPointDistribution( quals, 20,
Title='quality of random buildings');
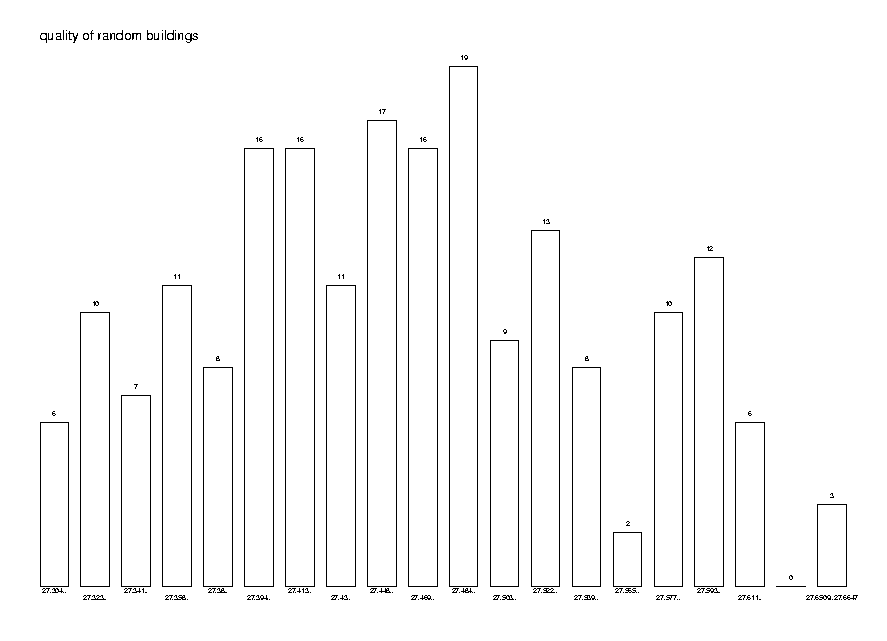
So the conclusion from this analysis is that it pays to construct several (around 10) random trees and select the best one.
© 2005 by Gaston Gonnet, Informatik, ETH Zurich
Last updated on Fri Sep 2 16:59:00 2005 by GhG