It is well known that coding DNA converts to mRNA and that the mRNA is translated into proteins with the mediation of tRNA molecules. The translation rules from DNA to mRNA are trivial. The Thymines (T) are changed to Uracils (U). The translation from mRNA to amino acids, for most forms of life, is governed by the genetic code.
?GeneticCode
GGG G Gly AGG R Arg CGG R Arg UGG W Trp GGA G Gly AGA R Arg CGA R Arg UGA Stop GGC G Gly AGC S Ser CGC R Arg UGC C Cys GGU G Gly AGU S Ser CGU R Arg UGU C Cys GAG E Glu AAG K Lys CAG Q Gln UAG Stop GAA E Glu AAA K Lys CAA Q Gln UAA Stop GAC D Asp AAC N Asn CAC H His UAC Y Tyr GAU D Asp AAU N Asn CAU H His UAU Y Tyr GCG A Ala ACG T Thr CCG P Pro UCG S Ser GCA A Ala ACA T Thr CCA P Pro UCA S Ser GCC A Ala ACC T Thr CCC P Pro UCC S Ser GCU A Ala ACU T Thr CCU P Pro UCU S Ser GUG V Val AUG M Met CUG L Leu UUG L Leu GUA V Val AUA I Ile CUA L Leu UUA L Leu GUC V Val AUC I Ile CUC L Leu UUC F Phe GUU V Val AUU I Ile CUU L Leu UUU F Phe See Also: ?AltGenCode ?BaseToInt ?CIntToAmino ?CodonToInt ?IntToBBB ?AminoToInt ?BBBToInt ?CIntToCodon ?Complement ?IntToCInt ?antiparallel ?BToInt ?CIntToInt ?GeneticCode ?IntToCodon ?AToCInt ?CIntToA ?CodonToA ?IntToB ?Reverse ?AToCodon ?CIntToAAA ?CodonToCInt ?IntToBase ------------
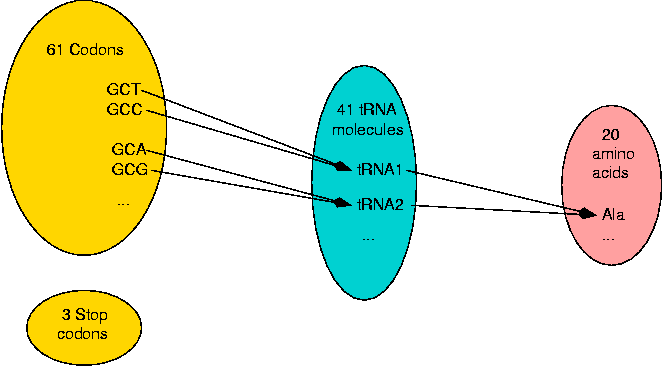
The groups of 3 nucleotides which are used for coding an amino acid or a stop signal are called codons. The amino acids which have more than one codon represent an ambiguity or redundancy which is not known to play a definitive role. Normally, each codon is translated by one tRNA molecule, although a tRNA molecule can translate more than one codon. There are 61 different codons, 41 tRNA molecules (for Saccharomyces cerevisiae, baker's yeast) and 20 amino acids. So the genetic code has two levels of redundancy.
The amino acids have particular frequencies which are correlated to the number of codons coding for it, but otherwise not uniform. The "Total Number of Pairs of Amino Acids" bio-recipe shows how to compute amino acid and pairs of amino acids frequencies. We will load the yeast database and compute these frequencies.
ReadDb( '/home/darwin/DB/yeast.db' );
Size := proc(x) t := SearchSeqDb(x); t[1,2]-t[1,1]+1 end:
for i to 20 do
s := Size(IntToA(i));
printf( '%13s %6d %.2f%%\n',
IntToAmino(i), s, 100*s/DB[TotAA] )
od:
Peptide file(/pub/projects/cbrg-oma-data/current/genomes/YEAST/yeast.db(12985775
), 6194 entries, 2902851 aminoacids)
Alanine 159685 5.50%
Arginine 129516 4.46%
Asparagine 176570 6.08%
Aspartic acid 168212 5.79%
Cysteine 38075 1.31%
Glutamine 113385 3.91%
Glutamic acid 189023 6.51%
Glycine 144464 4.98%
Histidine 62450 2.15%
Isoleucine 190412 6.56%
Leucine 278480 9.59%
Lysine 211892 7.30%
Methionine 60549 2.09%
Phenylalanine 131155 4.52%
Proline 125962 4.34%
Serine 261986 9.03%
Threonine 170558 5.88%
Tryptophan 30403 1.05%
Tyrosine 97413 3.36%
Valine 162661 5.60%
The RNA codons used are not uniformly distributed either. The departure of the codon frequencies is normally called codon bias. It is also true, and sort of a consequence of the above, that the tRNAs also have a biased distribution. We will use the DNA fields of the yeast database. to count the codon frequencies (a codon is 3 DNA/RNA bases in the correct reading frame).
Codons := CreateArray(1..64):
for e in Entries(DB) do
tD := SearchTag(DNA,e);
for i by 3 to length(tD) do
j := CodonToCInt( tD[i..i+2] );
Codons[j] := Codons[j]+1
od
od:
for i to 64 do
printf( ' %s %.2f%%', CIntToCodon(i), 100*Codons[i]/DB[TotAA] );
if mod(i,4)=0 then lprint() fi
od:
AAA 4.25% AAC 2.46% AAG 3.05% AAT 3.63% ACA 1.80% ACC 1.25% ACG 0.82% ACT 2.01% AGA 2.10% AGC 1.01% AGG 0.96% AGT 1.46% ATA 1.85% ATC 1.69% ATG 2.09% ATT 3.02% CAA 2.67% CAC 0.77% CAG 1.23% CAT 1.38% CCA 1.76% CCC 0.69% CCG 0.54% CCT 1.34% CGA 0.32% CGC 0.27% CGG 0.19% CGT 0.63% CTA 1.36% CTC 0.57% CTG 1.08% CTT 1.26% GAA 4.56% GAC 2.01% GAG 1.96% GAT 3.78% GCA 1.63% GCC 1.22% GCG 0.63% GCT 2.02% GGA 1.13% GGC 0.98% GGG 0.62% GGT 2.25% GTA 1.22% GTC 1.13% GTG 1.09% GTT 2.16% TAA 0.10% TAC 1.45% TAG 0.05% TAT 1.91% TCA 1.91% TCC 1.42% TCG 0.88% TCT 2.35% TGA 0.06% TGC 0.50% TGG 1.05% TGT 0.81% TTA 2.64% TTC 1.83% TTG 2.68% TTT 2.69%
The stop codons, TAA, TAG and TGA show frequency 0 as they never appear in a coding sequence. The DNA that we have recorded in this database is just the coding part. The most and least probable codons are quite far apart, if we sort the values (and ignore the 3 stop codons) we can compute the worst ratio:
sCodons := sort(Codons): sCodons[64] / sCodons[4];
24.1807
There is a factor of 24 between the least and most frequent codons.
To count the frequencies of the tRNAs we can use the results from the previously computed codon frequencies, but we need to use the tRNA translation table.
tRNAtable := [ [[GCT,GCC],[GCA,GCG],Ala], [[CGT,CGC,CGA],[CGG],[AGA],[AGG],Arg], [[AAT,AAC],Asn], [[GAT,GAC],Asp], [[TGT,TGC],Cys], [[CAA],[CAG],Gln], [[GAA],[GAG],Glu], [[GGT,GGC],[GGA],[GGG],Gly], [[CAT,CAC],His], [[ATT,ATC],[ATA],Ile], [[TTA],[TTG],[CTT,CTC],[CTA,CTG],Leu], [[AAA],[AAG],Lys], [[ATG],Met], [[TTT,TTC],Phe], [[CCT,CCC],[CCA,CCG],Pro], [[TCT,TCC],[TCA],[TCG],[AGT,AGC],Ser], [[ACT,ACC],[ACA],[ACG],Thr], [[TGG],Trp], [[TAT,TAC],Tyr], [[GTT,GTC],[GTA],[GTG],Val] ]:
From these tables we would like to create various functions which convert to and from codons, amino acids and tRNAs. This is done by the function SetuptRNA.
?SetuptRNA
Function SetuptRNA - set up functions for tRNA translations
Calling Sequence: SetuptRNA(d)
Parameters:
Name Type Description
-------------------------------------------------------
d list(list) a list (by aa) of list of codons or
d string the name of a known table of tRNA
Returns:
NULL
Global Variables: CIntTotInt_list IntTotInt_list ntRNA tIntToCInt_list
tIntToInt_list tIntTotRNA_list
Synopsis: This function sets up all the necessary functions to translate
tRNAs. These are from tInt to A, AAA, Amino, Int, CInt and Codon and from
Int and CInt to tRNA and tInt. Its input is either a string (which means a
predefined name) or it is a list of 20 (one per amino acid) lists of tRNAs.
The format is best given by an example, see the file lib/SetuptRNA.
Execution of SetuptRNA causes the following functions and values to be
defined:
Name Description
-----------------------------------------------------------------
ntRNA integer, the number of tRNA molecules used
-----------------------------------------------------------------
tIntToInt tInt (1..ntRNA) to Int (aa number, 1..20)
tIntToA tInt (1..ntRNA) to A (aa one-letter code)
tIntToAAA tInt (1..ntRNA) to AAA (aa 3-letter code)
tIntToAmino tInt (1..ntRNA) to Amino (aa full name)
-----------------------------------------------------------------
tIntToCInt tInt (1..ntRNA) to set of CInt (codon number, 1..64)
tIntToCodon tInt (1..ntRNA) to set of Codon (3-letter codon)
-----------------------------------------------------------------
tIntTotRNA tInt (1..ntRNA) to tRNA (tRNA name)
tRNATotInt tRNA (tRNA name) to tInt (1..ntRNA)
-----------------------------------------------------------------
IntTotInt Int (aa number, 1..20) to set of tInt (1..ntRNA)
IntTotRNA Int (aa number, 1..20) to set of tRNA (tRNA name)
-----------------------------------------------------------------
CIntTotInt CInt (codon number, 1..64) to tInt (1..ntRNA)
CIntTotRNA CInt (codon number, 1..64) to tRNA (tRNA name)
Currently the following names are recognized as arguments for SetuptRNA:
[Archaea, Bacteria, Eukaryota, eukaryotes, prokaryotes, YEAST, yeast]
Examples:
> SetuptRNA(yeast);
See also: ?ComputeTPI ?TPIDistr
------------
SetuptRNA( tRNAtable );
With these tables, which will also be used later, we can compute and print the tRNA frequencies of use. We place them in an array so that we can sort them and find their largest bias.
tRNA_freq := CreateArray(1..ntRNA):
for i to ntRNA do
for c in tIntToCInt(i) do tRNA_freq[i] := tRNA_freq[i] + Codons[c] od;
printf( 'tRNA %2d %s, %.2f%% %a\n', i, tIntTotRNA(i),
100*tRNA_freq[i]/DB[TotAA], tIntToCodon(i) )
od;
tRNA 1 Ala1, 3.24% {GCC,GCT}
tRNA 2 Ala2, 2.26% {GCA,GCG}
tRNA 3 Arg1, 1.21% {CGA,CGC,CGT}
tRNA 4 Arg2, 0.19% {CGG}
tRNA 5 Arg3, 2.10% {AGA}
tRNA 6 Arg4, 0.96% {AGG}
tRNA 7 Asn1, 6.08% {AAC,AAT}
tRNA 8 Asp1, 5.79% {GAC,GAT}
tRNA 9 Cys1, 1.31% {TGC,TGT}
tRNA 10 Gln1, 2.67% {CAA}
tRNA 11 Gln2, 1.23% {CAG}
tRNA 12 Glu1, 4.56% {GAA}
tRNA 13 Glu2, 1.96% {GAG}
tRNA 14 Gly1, 3.23% {GGC,GGT}
tRNA 15 Gly2, 1.13% {GGA}
tRNA 16 Gly3, 0.62% {GGG}
tRNA 17 His1, 2.15% {CAC,CAT}
tRNA 18 Ile1, 4.71% {ATC,ATT}
tRNA 19 Ile2, 1.85% {ATA}
tRNA 20 Leu1, 2.64% {TTA}
tRNA 21 Leu2, 2.68% {TTG}
tRNA 22 Leu3, 1.83% {CTC,CTT}
tRNA 23 Leu4, 2.44% {CTA,CTG}
tRNA 24 Lys1, 4.25% {AAA}
tRNA 25 Lys2, 3.05% {AAG}
tRNA 26 Met1, 2.09% {ATG}
tRNA 27 Phe1, 4.52% {TTC,TTT}
tRNA 28 Pro1, 2.04% {CCC,CCT}
tRNA 29 Pro2, 2.30% {CCA,CCG}
tRNA 30 Ser1, 3.77% {TCC,TCT}
tRNA 31 Ser2, 1.91% {TCA}
tRNA 32 Ser3, 0.88% {TCG}
tRNA 33 Ser4, 2.47% {AGC,AGT}
tRNA 34 Thr1, 3.26% {ACC,ACT}
tRNA 35 Thr2, 1.80% {ACA}
tRNA 36 Thr3, 0.82% {ACG}
tRNA 37 Trp1, 1.05% {TGG}
tRNA 38 Tyr1, 3.36% {TAC,TAT}
tRNA 39 Val1, 3.29% {GTC,GTT}
tRNA 40 Val2, 1.22% {GTA}
tRNA 41 Val3, 1.09% {GTG}
The ratio between the most frequent and less frequent is:
max(tRNA_freq) / min(tRNA_freq);
32.2856
Autocorrelation of codons, tRNA or amino acids
Why is autocorrelation relevant? Autocorrelation measures the reuse of a particular codon/tRNA as contrasted with its use. E.g. a codon may be very rare, that is it appears with low frequency, but it could be highly autocorrelated, i.e. it is very likely to appears in tandems. In terms of reloading tRNA molecules or simply having the tRNA available, autocorrelation of codons/tRNA will give us an indication of whether this is a relevant process for the regulation of protein synthesis.
Besides their biased frequencies, codons, tRNA and amino acids show signs of autocorrelation. Autocorrelation is a departure of the expected frequency when we know the previous symbol. In other words, the frequencies of pairs are not the same as the product of the individual frequencies. It is of particular interest to study the autocorrelation of the codons coding for one particular amino acid or the tRNAs coding for one particular amino acid. Notice that within the codons or tRNA coding for a particular amino acid, there can be no natural selection pressures as the proteins produced are the same.
We will now compute the codon autocorrelation for serine. Serine is coded by the following codons and tRNA:
tRNAtable[ AToInt(S) ];
[[TCT, TCC], [TCA], [TCG], [AGT, AGC], Ser]
For this autocorrelation we will take one protein (database entry) at a time. We will not correlate amino acids between different proteins (last of one with first of the next one), as we have no information about the order of the proteins within the yeast genome (there are also other good reasons for not doing this). It is simpler to do it for all amino acids in one pass, we just keep an array of 20 entries with the information of the previous codon used by each protein. Notice that we should skip any stop codon that we encounter which are coded as amino acid number 22.
Cod_Cod := CreateArray(1..64,1..64):
for e in Entries(DB) do
tD := SearchTag(DNA,e);
prev := CreateArray(1..20);
for i by 3 to length(tD) do
j := CodonToCInt( tD[i..i+2] );
k := CIntToInt(j);
if k = 22 then next
elif prev[k] > 0 then
Cod_Cod[prev[k],j] := Cod_Cod[prev[k],j]+1 fi;
prev[k] := j;
od
od:
Now we print the portion of the matrix corresponding to serine.
for i to 64 do if CIntToA(i)='S' then
printf( '%s ', CIntToCodon(i) );
for j to 64 do if CIntToA(j)='S' then
printf( '%6d', Cod_Cod[i,j] ) fi od;
printf( '\n' )
fi od;
AGC 4001 5260 5487 4035 2757 6888 AGT 5282 7553 8544 6008 3883 9957 TCA 5755 8704 12409 8231 5468 13571 TCC 4171 6136 8097 6856 3874 11057 TCG 2923 3909 5396 3976 2765 6132 TCT 6476 9771 14028 11131 6260 19044
From the counts alone it is difficult to see the autocorrelation. The different codons have different frequencies. To see the autocorrelation we will subtract the expected values of the counts and divide by the standard deviation. This is what is called a z-transform, and it has the advantage of revealing how far from expected our results are. In Np we will store the total number of pairs of codons. The probability of a pair appearing is the product of the individual probabilities, divided by the probability of having a serine (this is because the pairs are counted exclusively among the serines). After a simple cancellation we obtain the formula below.
Np := sum(sum(Cod_Cod));
for i to 64 do if CIntToA(i)='S' then
printf( '%s ', CIntToCodon(i) );
for j to 64 do if CIntToA(j)='S' then
pr := Codons[i]/DB[TotAA] * Codons[j]/Size(S);
std := sqrt( Np*pr*(1-pr) );
printf( '%7.2f', ( Cod_Cod[i,j] - Np*pr ) / std ) fi od;
printf( '\n' )
fi od;
Np := 2780865 AGC 15.33 10.69 -5.73 -5.68 0.19 -4.97 AGT 11.02 12.26 -0.23 -4.61 -1.37 -5.95 TCA -2.24 1.50 11.62 -1.01 3.98 -1.92 TCC -3.63 -3.00 -2.48 8.41 0.27 7.79 TCG 3.36 -0.96 2.98 1.92 7.42 -3.27 TCT -9.80 -7.76 1.98 8.53 -1.67 15.56
We can see that there are obvious signs of autocorrelation, the diagonal values are all positive and almost always the largest for their columns/rows. There are also signs of tRNA autocorrelation. If we observe that codons AGC,AGT are translated by the same tRNA and ditto for codons TCC,TCT we see autocorrelation also at the tRNA level.
The above analysis of autocorrelation suffers from a bias that may be induced by different base frequencies in different parts of the genome. It is known that some parts of the genome are GC rich while other parts are GC poor. Such long-streched biases induce an autocorrelation in the codons, which could be significant.
So we would like to measure the autocorrelation in a way that is independent of the base composition. Furthermore it would be nice to be able to "add" together the autocorrelations of different amino acids. To meet these goals we have defined the TPI (tRNA Pairing Index).
tRNA Pairing Index for a given amino acid
The TPI is an index which is computed for each protein and measures how autocorrelated (positively or negatively) are its codons. Is is completely independent of the frequencies of the amino acids, tRNA or codons, so it will not suffer from any of the common sources of bias.
The way of measuring the autocorrelation independently of everything else is by transforming the problem into a combinatorial one. For example, suppose that we are considering an amino acid X which occurs 7 times in a protein and can be translated by two tRNAs, A and B (e.g. 3 A's and 4 B's). We will extract the tRNAs from our sequence and represent them as a sequence of 7 symbols. E.g. AABABBB.
Highly autocorrelated cases are AAABBBB and BBBBAAA. A highly negatively autocorrelated case is BABABAB. This autocorrelation can be quantified by the number of identical pairs in the sequence or, conversely, by the number of changes (nc) as we read from left to right. Notice that for a sequence of length n, the number of identical pairs plus the number of changes is n-1. The mathematics is completely analogous for the number of pairs or number of changes. We call these breaks in the sequences changes, with the thought that if a tRNA molecule is doing the translation for one particular amino acid, when these breaks happen, this tRNA will have to be changed for another molecule. The first two examples have 1 change each, the last example has 6 changes. The TPI measures how high the actual number of pairs are or how low the nc is compared to all possible permutations of the sequence of tRNAs. In this case we have 35 cases:
| sequence/nc | sequence/nc | sequence/nc | sequence/nc | sequence/nc |
| AAABBBB 1 | AABABBB 3 | AABBABB 3 | AABBBAB 3 | AABBBBA 2 |
| ABAABBB 3 | ABABABB 5 | ABABBAB 5 | ABABBBA 4 | ABBAABB 3 |
| ABBABAB 5 | ABBABBA 4 | ABBBAAB 3 | ABBBABA 4 | ABBBBAA 2 |
| BAAABBB 2 | BAABABB 4 | BAABBAB 4 | BAABBBA 3 | BABAABB 4 |
| BABABAB 6 | BABABBA 5 | BABBAAB 4 | BABBABA 5 | BABBBAA 3 |
| BBAAABB 2 | BBAABAB 4 | BBAABBA 3 | BBABAAB 4 | BBABABA 5 |
| BBABBAA 3 | BBBAAAB 2 | BBBAABA 3 | BBBABAA 3 | BBBBAAA 1 |
We can compute the probability of a given nc happening. This is the number of times they happen divided by 35 (each of the permutation is equally likely to happen). The following histogram shows the distribution of the nc. From such a curve we can judge how rare or common a given nc is.
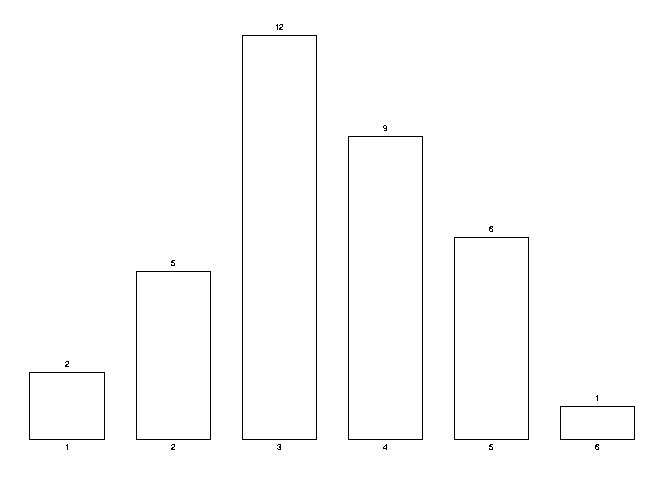
Computation of the probability of the number of changes (nc)
We will now write a function to compute the probability and cumulative distribution of a given nc. This is a fairly mathematical and computational problem, and some readers may want to skip to the section where the TPI is computed.
It is easy to observe that the probability of the number of changes (nc) does not depend on what the symbols are, but rather depends on how many of each. We will write a function, called nc, that computes the probability of a having a given nc from a random permutation. This function will be based on another function, called nc_r, which does the recursive part of the computation. Nc_r assumes that we are not at the beginning of the sequence, but rather that the last symbol observed is known. To identify this known symbol (all symbols are otherwise equivalent), we will make it the first of the arguments. Our function nc_r assumes that it is called with a symbol of the first class preceeding the n1+n2 other symbols.
nc_r := proc( nc:integer, n1:integer, n2:integer )
If any of the arguments is negative or if more changes than symbols are exptected, then the answer is 0.
if n1 < 0 or n2 < 0 or nc < 0 or nc > n1+n2 then 0
if there are no more symbols (and nc must be 0) then the probability is 1.
elif n1=0 and n2=0 then 1
Now we recurse. The first symbol is either from the class of n1 (no change) or from the class of n2, in which case now the preceeding symbol is of the second class and we invert the arguments.
else n1/(n1+n2) * nc_r( nc, n1-1, n2 ) +
n2/(n1+n2) * nc_r( nc-1, n2-1, n1 )
fi
end:
Testing it with the above example, computing the probability of 3 changes assuming that the previous symbol was an A:
nc_r( 3, 3, 4 ) * 35;
9.0000
There are 6 cases starting with A which have 3 changes and 3 cases starting with B with 2 changes. This coincides with the probability computed (once multiplied by 35). Before we resolve the original problem we will generalize nc_r to be able to handle any number of groups of symbols. In our application we may have up to 4 symbols (yeast has some amino acids which are translated by 4 different tRNA molecules). Also, the code as written above, is badly exponential. We could use ideas from dynamic programming to speed it up. In this case it is much simpler to use the remember function to avoid recomputing cases.
?remember
Function remember - evaluate a function and remember its result Option: builtin Calling Sequence: remember(func_call) Parameters: Name Type Description --------------------------------------- func_call structure a function call Returns: anything Synopsis: The remember function stores results of function evaluations in an internal table for the purpose of saving computation time. When remember is called, the system checks to see if the argument function has been called previously with the same arguments, and if so, then the previous result is returned. If it is not found, the function call is executed and its result stored in the internal table as well as returned to the user. The internal table does not keep all the results forever, at garbage collection time arguments that are no longer available will cause the corresponding entries to be removed. Eventually, all unused entries will be removed. The user of remember should keep in mind that this is a heuristic saving of evaluations, it should not be counted on happening every time. Remember is usable when the argument function does not have side effects (for example printing), as it will be unpredictable when these side effects will happen. It should also be used on functions which do a significant amount of computation, else its effort is not justifiable. The profiling tools are good to determine which functions will profit from remembering. Warning: When the returned value is a structure (e.g. a matrix or a class), changing the structure will also change value stored in the remember-table! This will lead to unexpected behaviour. In case that the user wants to erase the remember table, (for example the function to be remembered has changed its behavior in some way and old values should not be remembered), calling remember with the argument "erase" will erase all previously remembered values For the example below we compute the Fibonacci numbers with their simple recurrence. Without the remember function, this definition takes exponential time. Examples: > F := proc( n:integer ) if n < 2 then n else remember(F(n-1)) + remember(F(n-2)) fi end: > [ seq( F(i), i=0..10 )]; [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55] > F(50); 12586269025 See also: ?hash ?profiling ?table ------------
The code has a few other optimizations which are intended to reuse previous computations as much as possible and to cut useless computation as early as possible. One of the ways of reusing the previous results as much as possible is to keep the 2nd to last sizes (3rd to last argument) in increasing order. (The order of these arguments does not matter, only the first is relevant).
nc_r := proc( ch:integer, n1:integer, n2:integer ) n := sum( args[i], i=2..nargs );
resolve as many trivial cases as possible
if min(args) < 0 or ch > n or ch > 2*(n-max(args[2..nargs])) + 1 then 0 elif max(args) = 0 then 1 elif nargs >= 3 and n2=0 then nc_r(ch,n1,args[4..nargs])
if any of the args[3..nargs] are out of order, reorder them and call recursively
else for i from 3 to nargs-1 do if args[i] > args[i+1] then return( nc_r( args[1..i-1], args[i+1], args[i], args[i+2..nargs] )) fi od;
compute recursively (remember/reuse previous values)
r := n1/n * remember( nc_r( ch, n1-1, args[3..nargs] ));
for i from 3 to nargs do
r := r + args[i]/n * remember( nc_r( ch-1, args[i]-1,
args[2..i-1], args[i+1..nargs] ))
od;
r
fi
end:
Warning: procedure nc_r reassigned
Now we can write our main function to compute the probability of a given nc. To make coding simpler, we assume we have an extra symbol which appears 0 times and is preceeding our sequence. This works correctly unless we have the exceptional case of no changes and no symbols at all. The function becomes:
nc := proc( ch )
if {args}=0 then 1 else nc_r( ch+1, 0, args[2..nargs] ) fi end:
and we can test it with a more significant example, say 7 and 10 symbols:
DrawHistogram( [ seq( nc(i,7,10), i=1..17 ) ] );
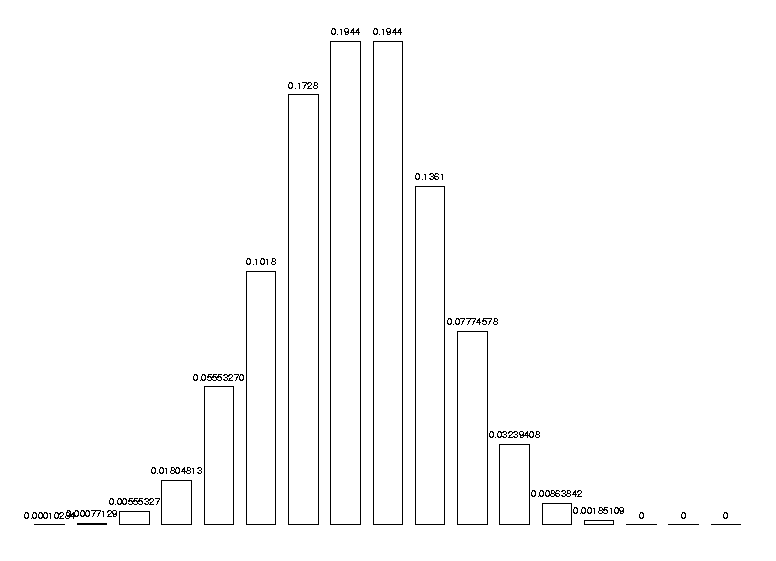
It is wise to check that the probabilities add up to 1:
sum( nc(i,7,10), i=1..17 ) - 1;
-1.1102e-16
the difference to 1 is well within round-off errors.
Due to the importance of this function in our research and its complexity for large arguments, it has been implemented in the kernel to make it faster and more compact. The kernel function is called TPIDistr and computes the entire distribution of the nc for a given set of number of symbols. For example:
DrawHistogram( TPIDistr(5,10,20,30) );
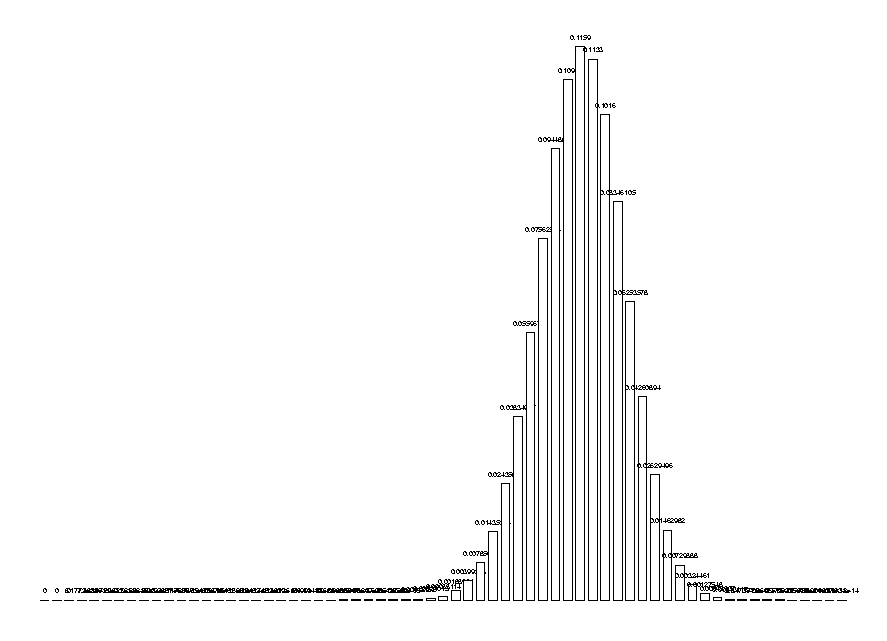
Finally, to estimate how rare a given nc is, we need to compute its cumulative distribution. Since the distribution is over the integers, we will take the cumulative distribution which adds one half of the probability at the point. (The second to last arguments of this function are the numbers of each symbol.)
nc_cum := proc( ch:integer ) d := TPIDistr(args[2..nargs]); if ch < 0 then 0 elif ch >= length(d) then 1 else d[ch+1] / 2 + sum( d[1..ch] ) fi end: nc_cum(3,7,10);
0.00365076
Computing the TPI for all the amino acids in a given entry
The previous computation was designed to find how common/rare is a particular number of changes for a single amino acid. When we study a database entry, we would like to take all the amino acids and somehow summarize all the pairs/changes information into a single index. To do this we will consider that an nc is the unit to measure and we will add the nc's of all the amino acids. The distribution of the sum of all the nc's is the convolution of the individual distributions for each amino acid.
The previous computation was designed to find how common/rare is a particular number of changes for a single amino acid. When we study a database entry, we would like to take all the amino acids and somehow summarize all the pairs/changes information into a single index. To do this we will consider that an nc is the unit to measure and we will add the nc's of all the amino acids. The distribution of the sum of all the nc's is the convolution of the individual distributions for each amino acid.
Darwin has a function which does this computation for a given Entry called ComputeTPI. The Entry has to contain DNA information for this to be possible. ComputeTPI computes the number of pairs/changes for each amino acid and the total number. Then computes the distribution of the pairs/changes for each amino acid and convolves the distributions. Finally it computes the cumulative probability. Two indices, mathematically equivalent, are returned from this cumulative probability. The first one is just a normal N(0,1) deviate with the same cumulative probability. The second is just the cumulative distribution linearly spread over the interval -1 ... 1. We test the function against an arbitrary Entry:
ComputeTPI( Entry(9) );
[1.2222, 0.7783]
Darwin has a function which does this computation for a given Entry called ComputeTPI. The Entry has to contain DNA information for this to be possible. ComputeTPI computes the number of pairs/changes for each amino acid and the total number. Then computes the distribution of the pairs/changes for each amino acid and convolves the distributions. Finally it computes the cumulative probability. Two indices, mathematically equivalent, are returned from this cumulative probability. The first one is just a normal N(0,1) deviate with the same cumulative probability. The second is just the cumulative distribution linearly spread over the interval -1 ... 1. We test the function against an arbitrary Entry:
ComputeTPI( Entry(9) );
[1.2222, 0.7783]
We now compute the univariate and covariate statistics of the TPI indices for a few random entries.
cov := Covariance( 'TPI index', [normal,'-1...1'] ): to 100 do cov + ComputeTPI( Rand(Entry) ) od: print( cov );
Covariance analysis for TPI index, 100 data points
normal -1...1
Means 0.1284 0.0572
Covariance matrix
normal 0.9110
-1...1 0.5252 0.3137
and we see that the TPI indices are correlated and their means are positively biased. (This is also true for the entire yeast genome). This means that there is a positive autocorrelation of tRNA completely independent of their frequencies.
© 2015 by Gaston Gonnet, Informatik, ETH Zurich
Please cite as:
@techreport{ Gonnet-TPI,
author = {Gaston H. Gonnet},
title = {The tRNA Pairing Index},
month = { April },
year = {2003},
number = { 399 },
howpublished = { Electronic publication },
copyright = {code under the GNU General Public License},
institution = {Informatik, ETH, Zurich},
URL = { http://www.biorecipes.com/TPI/code.html }
}
Last updated on Thu Dec 10 09:54:20 2015 by GhG
!!! This document is stored in the ETH Web archive and is no longer maintained !!!